Skivefres hors de la carte

Man kan i dag få kjøpt verktøy til å gjøre det meste av det man trenger å gjøre, men det hender at det verktøyet man behøver ikke er å få tak i, eller operasjonen man skal utføre er særdeles sær og spesifikk. Da kan det være nødvendig å lage sitt eget.

En slik situasjon dukket opp for meg for en stund siden, og jeg ble nødt til å lage min egen skivefres til ett kutt jeg skulle gjøre i en del.

Hovedproblemet var at jeg skulle gjøre dette manuelt, og ikke i en CNC maskin, der dette ikke hadde vært et problem siden jeg kunne løst det med en kombinasjon av verktøybaner, men siden dette skulle gjøres for hånd så var jeg avhengig av en spesiell form på verktøyet.

Å lage et spor eller slisse i en del er én ting, men jeg trengte en spesifikk radie kuttet inn i en del med en gitt sporbredde. Selve bredden kunne jeg riktignok oppnådd med flere passeringer av et tynnere verktøy, men ingen verktøy jeg hadde var av riktig diameter.

Så når jeg skulle lage mitt eget så var det to hovedpunkter å ta hensyn til; diameteren og tykkelsen. Tykkelsen gir seg selv, det er ikke noe poeng å lage verktøyet tynnere enn sporet - innenfor rimelighetens grenser selvsagt - et tynt verktøy som må ta mer enn én passering vil bøye seg dersom det ikke har støtte fra begge sider som hindrer defleksjon. Sporet skulle bli 1,4mm tykt, så da er det tykkelsen jeg lager verktøyet. Hadde kuttet vært så bredt at det hadde begynt å bli et problem for maskinen å drive verktøyet - større kuttbredde fører selvsagt til økt belastning - måtte man jo lagd et tynnere verktøy som passerte flere ganger, men da hadde verktøyet vært så tykt at strukturell stabilitet ikke ville vært et problem.

Radien i sporet jeg skulle lage var 12,5mm, altså måtte jeg lage et verktøy på 25mm.

Jeg bestemte meg for å lage en skivefres med utbyttbare skiver. Hovedsakelig fordi selve fresen blir enklere å lage og lettere å herde når den ikke har en integrert stamme, men også fordi jeg da i fremtiden har en holder til andre freser dersom jeg blir nødt til å gjøre det samme igjen med andre former. Ulempen er at jeg da ender opp med en strammeskrue på undersiden som i noen tilfeller kan være et problem for framkommeligheten til verktøyet.

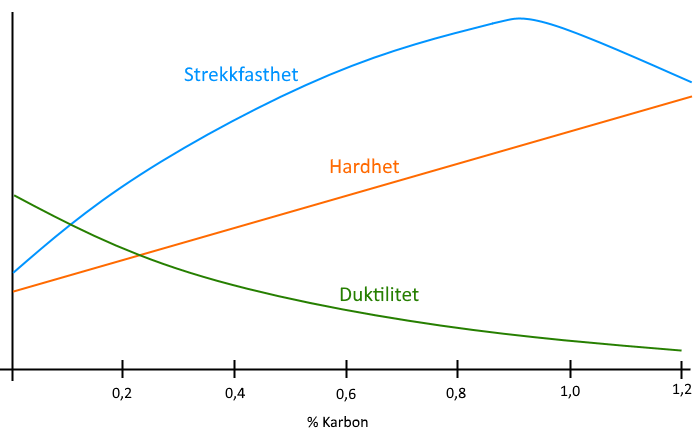
Jeg hadde to valg når det kom til stål; enten lage den av et lavkarbonstål og settherde den, eller gjennomherde et høykarbonstål. Jeg hadde ikke enkel tilgang til settherding da jeg lagde den, så jeg valgte å lage den av et høykarbonstål. Jeg brukte Uddeholm Arne stål, som har et karboninnhold på 0,95%, som gjør det særdeles herdbart. Det er egentlig ikke et verktøystål for kutteverktøy, men det gjør jobben.

Jeg begynte med å tegne opp fresen i CAD (Computer Aided Design, DAK på norsk (DataAssistert Konstruksjon)), i motsetning til CAM (Computer Aided Manufacturing), DAP når norsk (DataAssistert Produksjon).

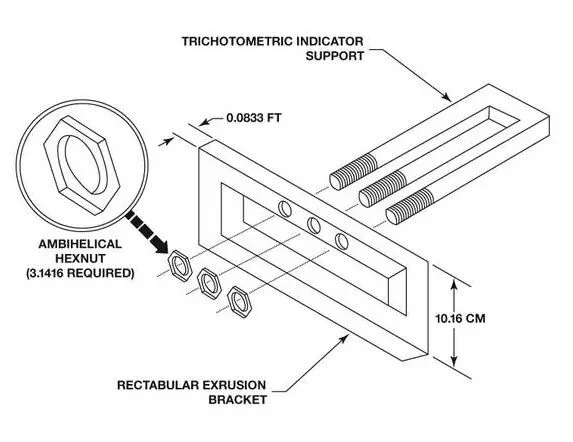
Deretter dreide jeg startmaterialet, et par millimeter tykkere enn jeg trengte slik at det opprettholdt formen sin gjennom etterfølgende operasjoner, samt en stamme for oppspenning i delehodet. Som vi ser på bildet over så planla jeg å bore 3mm hull til tennene så det skulle bli mindre materiale å slipe meg gjennom etter herding, så diameteren på dette tidspunktet var rundt 28mm.

Over ser vi skivefresen før herding. Dette er egentlig den andre jeg lagde, den første ble ikke ordentlig hard, eller rettere sagt, den ble hard, men jeg hadde ikke nok materiale igjen til sliping etter herding, så de to 1mm målene du ser på CAD bildet over representerer materialet pinnefresen lar være igjen før herding, mer om det senere.

Jeg boret hullene i bunnen av tennene, deretter vinklet jeg delehodet 90° og freste vekk resten av det overflødige materialet. Jeg satte den så tilbake i dreiebenken og kappet av stammen som kun var til for å holde den i delehodet. Så planslipte jeg den raskt ned til 1mm tykkere enn du skulle bli etter herding, slik at jeg hadde 0,5mm på hver side, og for å opprettholde retthet under herding var det viktig at den var plan og flat og ikke trakk seg sammen ujevnt ved nedkjøling.

Under er et bilde av den første jeg lagde.

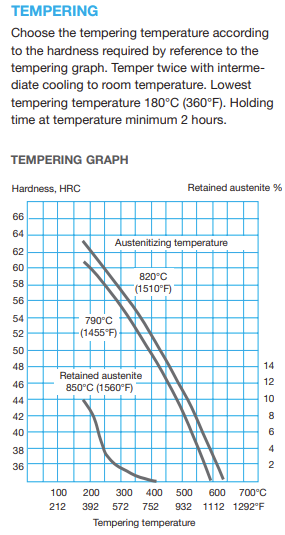
Problemet med mitt første forsøk over var at, (som vi ser på retningslinjene for herding av dette stålet til høyre) jeg ikke hadde mulighet til å hindre dekarborisering under herdeprosessen, enten ved å;

• pakke biten i rustfri stålfolie for å hindre oksygentilgang

• settherdingsboks

• inert atmosfære (som enten å varme opp i et vakuum eller nitrogenfylt kammer)

• anti-glødeskall pasta

Anti-glødeskall pasta.

Stålfolie for å danne en liten oksygenfri atmosfære.

Settherding med kasenitt er i bunn og grunn det samme som anti-glødeskall pasta, men med karbon i som blir tilført overflaten.

Den første jeg lagde valgte jeg å varme på 800 °C i 30min, per anbefalingene over. Men siden jeg bare hadde latt det være igjen et par tidels millimetere igjen til sliping etter herding ble for mye av stålet om til glødeskall.

Glødeskall, et resultat av å bli oppvarmet for lenge i en oksygenholdig atmosfære.

Jeg forsøkte å slipe den ned til korrekte dimensjoner, men som vi ser under så hadde for mye av karbonet i overflaten brent ut, slik at kuttsidene ikke ble skarpe i det hele tatt.

Ingen kutteevne, bare dytter materialet til side.

For å få den til å kutte måtte jeg slipe meg ned til hardhet, men det førte også til at den ikke lenger var 25mm i diameter.

Ingen voldsom suksess… Den kuttet, men nå var den jo for liten.

Forsøk Nr.2

Som jeg har nevnt tidligere i andre innlegg, så kan det være et problem at noe ikke er gjennomherdet. Det er ikke et like viktig moment her, det er mye viktigere at verktøyet er hardt ytterst. Det er selvsagt ønskelig at den er gjennomherdet, men med en så tynn del er det ikke et problem. Det som derimot var det største problemet mitt, var som sagt at jeg ikke hadde mulighet til å beskytte delen mot dekarborisering / oksidering. Så løsningen ble da å la det være igjen såpass mye materiale at stålet selv ble en beskyttelse mot dekarborisering lenger inn i materialet.

Så til forsøk nr.2 lagde jeg pre-herding skiven større i alle retninger, og økte herdetemperaturen, men halverte liggetiden, i følge herdedataene.

Etter herding var det rett i anløpningsovnen.

Jeg anløpte ved 200 °C i de anbefalte minimum 2 timene, men kun én gang, for jeg var redd for å miste for mye hardhet.

Deretter var den klar for sliping.

Plansliping.

Jeg brukte en bit sølvstål til å indeksere den planslipte delen igjen, slik at jeg visste hvor den stod i forhold til tegningen og hvor mange grader jeg skulle vri delehodet.

Sliping med carborundum-kopp

På tide med en liten test.

Se det var bedre ja!

Den endte opp med å gjøre jobben ypperlig.

Alle varmebehandlingsdata i dette innlegget er hentet fra Uddeholms datablader om dette spesifikke stålet, her.

Stål: Krystaller og mikrostrukturer

Så og si alle metaller og ikkemetaller er krystalliske i natur, som vil si at de har en meget organisert og stabil måte å arrangere atomene sine og deres bindinger på. Krystaller er geometrisk ordnede atomer i ulike varianter.

Når stål går fra varmt til kaldt og stivner forekommer det nukleasjon av jernet rundt urenheter i blandingen. Disse urenhetene fungerer som katalysatorer og atomene vil aggregere sammen i klynger. Disse gror til korn av homogene krystaller og fortsetter å gro i en geometrisk ordnet struktur til de treffer en annen krystall, som mest sannsynlig ikke har den samme orienteringen som seg selv, og en grense vil skapes mellom disse kornene.

Med mikrostruktur menes en struktur som kun kan observeres med mikroskop.

Disse korngrensene er i utgangspunktet en generell plan-defekt i materialet som skiller regioner av krystaller med ulik orientering innen et polykrystallinsk materiale.

View fullsize

Disse defektene begrenser termisk og elektrisk ledeevne i materialet. Man skulle altså tro at optimalt sett ville vi gjerne hatt en homogen blokk med materiale bestående av ett korn med én gjennomgående krystallstruktur, men det er ikke tilfellet. For det første er det så godt som uoppnåelig, og problemet med at atomene ordner seg i slike geometriske strukturer er at krystallene blir spesielt svake mot skjærbelastning som går parallelt med krystallstrukturen. Dette er kjent som “slip planes“, skliplan eller skjærflater, og avhengig av krystallstrukturen har et antall belastningsretninger som krystallene er spesielt svake mot.

Skjærbelastninger som forekommer parallelt med krystallets skjærplan har mye lettere for å deformere krystallet enn belastninger som ikke går langs ett av disse planene. Det finnes flere varianter av disse planene avhengig av krystallstrukturen:

View fullsize

Over er eksempel på skjærplan for strukturene enkel kubisk (SC), kropps-sentrert kubisk (BCC) og flatesentrert kubisk (FCC), fra venstre til høyre. Det finnes mange av disse planene avhengig av struktur, og det er et tema innen metallurgien vi ikke behøver å bevege oss inn på nå, men så vidt jeg forstår så refererer tallene til hvilken akse atomene som faller innen skjærplanet befinner seg på og retningen, binært fra 0 til 1 i XYZ.
Forskjellen på disse er hvordan atomene pakker seg i krystallene og kan visualiseres slik:

View fullsize

Disse skjærplanene går alltid gjennom der atomene er tettest pakket sammen, siden de der har lettere for å dytte på hverandre uten “slark“ og oppstår som regel gjennom det største av disse planene som koinsiderer med belastningen på krystallet siden disse planene blir “truffet” først.

Forskyvninger har lettere for å oppstå langs de grønne pilene enn de rød.

En slik forskyvning (eng.: dislocation) stanser når den møter en korngrense. Krystallet kan ikke deformeres ytterligere siden belastningen nå har gått gjennom det første krystallet, truffet en grense til et annet krystall med en struktur som ikke lar seg forskyve like lett langs denne vektoren.

Jern og karbon er aldri i en fullstendig løsning med hverandre i avkjølt tilstand, men blander seg i form av “granuler“ eller “korn“. Disse kornene er krystaller i ulike størrelser og former som sammen utgjør det hele materialet. Disse krystalliske klyngene kan inneholde ulike blandinger av jern og karbon, men binder seg normalt ikke som molekyler i et nytt materiale, med unntak.

Karbonmengden i stålet er av betydning fordi den bidrar til å lage sterkere korngrenser i form av jernkarbid, og siden karbonatomene er mindre enn jernatomene kan de også oppta plasser inni krystallene. Dette kalles en punkt-defekt og gjør at atomene i krystallet har mindre rom og/eller forskyver den interne strukturen i krystallet, som gjør den mer motstandsdyktig for deformasjon.

View fullsize

Siden de geometriske planene i kornene er de svake punktene i materialet er det bedre å ha mange små grenser som går i alle mulige retninger enn å ha et par store krystaller. Små korn har en større grenseoverflate i forhold til volumet slik at det eksisterer flere grenser og bindinger med ulik orientering enn i et liknende volum med større krystaller, slik at en potensiell forskyvning har mindre effekt siden færre forskyvninger kan finne sted i et mindre korn. Mange små korn er generelt sett betraktet som et bedre materiale siden rettede belastninger blir jevnet ut mellom alle de ulikt orienterte krystallene.

View fullsize

Styrken til materialet kan forbedres ved å endre på kornstørrelsene og korngrensene.

Ved korngrenseforsterkning fungerer korngrensene som låsepunkter som hindrer ytterligere forskyvningsforplantning. Siden strukturen til tilstøtende korn varierer i orientering, krever det mer energi for en forskyvning å endre retning og bevege seg inn i neste korn. Korngrensen er også mye mer kaotisk enn kornet, som forhindrer at forskyvningene beveger seg i et kontinuerlig plan. Forminskelse av denne forskyvningen vil hindre at plastisk deformasjon oppstår, og dermed øke bruddstyrken til materialet.

Under en påført belastning vil eksisterende forskyvninger bevege seg gjennom krystallstrukturen inntil det støter på en korngrense, hvor den store ulikheten mellom forskjellige korn skaper et frastøtende stressfelt for å motvirke ytterligere forskyvning. Ettersom flere forskyvninger forplanter seg til denne grensen, oppstår en opphopning av stress i en klynge som ikke er i stand til å bevege seg forbi grensen. Når nok stress er blitt hopet opp på et punkt vil det til slutt overkomme motstanden i korngrensen og forplante seg videre i neste korn og ytterligere deformasjon oppstår.

View fullsize

Ved å redusere kornstørrelsen reduserer man mengden mulig stress-samling ved grensen, og øker mengden av påført belastning som er nødvendig for å bevege en forskyvning over en korngrense.

Jo høyere den nødvendige belastningen for å flytte forskyvningen, desto høyere bruddstyrke. Dermed er det da et omvendt forhold mellom kornstørrelse og bruddstyrke, som demonstrert av Hall-Petch-ligningen.

Imidlertid, når det er en stor retningsendring i orienteringen til to tilstøtende korn, kan forskyvningen ikke nødvendigvis bevege seg fra ett korn til det andre, men i stedet skape en ny fordelingskilde i tilstøtende korn. Teorien forblir den samme at flere korngrenser skaper mer motstand til dislokasjonsbevegelse, og igjen styrker materialet.

Det er av denne grunn det er ønskelig med små og godt sammenblandede korn i stålet og ikke store korn. Når det er sagt, er det naturligvis av denne grunn også vanskeligere å bearbeide et slikt materiale, og rent jern skaper vanligvis ganske store krystaller, som vi nå forstår gjør det enklere å deformere og forme. Dette gjelder selvsagt innenfor et område av størrelser, og dersom krystallene blir veldig store blir det igjen vanskelig å forme materialet på en meningsfylt måte. Dersom en teoretisk stang hadde hatt to store krystaller som på ett punkt langs lengden var den eneste bindingen i stangen, ville den ikke være veldig enkel å forme, men brekke ganske lett.

Pyritt (jernsulfid), ikke et godt eksempel på jernkrystaller, men et kult bilde for å illustrere hvor store krystaller kan gro under rette forhold.

Hall-Petch forholdet gjelder stort sett for korn fra 1mm til 10 nm. Det var trodd at dette forholdet mellom kornstørrelse og bruddstyrke var uendelig videreførbart, men under 10 nanometer vil bruddstyrken holde seg lik eller synke igjen, og over 1mm gjelder det samme.

Det er flere andre variabler som bestemmer duktiliteten og styrken i stålet mer enn kornstørrelsen (slik som karbonmengde), men disse fungerer ikke som de skal uten en passende kornstørrelse å jobbe med.

Varmebehandling av stål, hvis metoder vi skal se nærmere på i neste innlegg, hovedsakelig herding, er rett og slett metoder for å endre typene, sammensetningene og ikke minst størrelsene på kornene i materialet.

Så, hvilke typer mikrostrukturer finnes i stål og hvordan oppstår de?

Faser, mikrostrukturerer og karbonets effekt

Når rent jern begynner å stivne fra flytende form (over 1539 °C ) og atomene binder seg og nukleasjon forekommer, vil krystallene forme seg i en kropps-sentrert (BCC) struktur.

Kropps-sentrert kubisk krystall (BCC). Så kalt fordi enheten blir definert med et atom i hvert hjørne og ett i midten av kuben. En mindre tettpakket struktur enn FCC. Har plass til å inneholde mer karbon enn FCC.

Etter en stund med krystallisering og temperaturen synker til 1392 °C forekommer en merkelig ting. Temperaturen slutter å synke i en liten periode som om den blir varmet opp innenfra. Dette er også det som skjer ved at krystallstrukturen reorganiserer seg til en flate-sentrert (FCC) struktur. Dette er en eksotermisk reaksjon slik at den produserer litt varme selv og vil derfor virke som temperaturen står stille i et øyeblikk.

Flate-sentrert kubisk krystall (FCC). Så kalt fordi enheten blir definert med et atom i hvert hjørne og ett i senter av hver flate. En tettpakket struktur som har plass til å inneholde mindre karbon enn BCC.

Dette kalles et kritisk punkt (eng.: arrest point) og forekommer flere ganger i nedkjølingen. Det kan virke rart at det skjer, for selv om materialet er varmt er det allikevel solid.

Men dersom vi kunne se ting fra atomets perspektiv ville det ikke vært så overraskende. Materialer er stort sett tomrom og avstanden mellom atomene er relativt stor. La oss ikke begi oss ut på atomteori og hvorfor ting i det hele tatt velger å henge sammen, men de har ihvertfall plass til å bevege seg. De kan ikke skyte rundt som de er i stand til i en væske eller gass, men ved å tilføre energi i form av varme kan vi motivere krystallene til å reorganisere seg.

View fullsize

Solidifiseringsprosessen; nukleasjon rundt urenheter (a), ekspandering av de enkelte krystallene (b), danning av kornene (c), korngrenser dannes og et polykrystallinsk materiale oppstår (d).

Herdetemperaturer og andre behandlingstemperaturer er ofte oppgitt rundet av til nærmeste 10°C. Hopp på 10 grader er det mest praktiske temperatursteget å bruke for å endre resultatet av varmebehandling. Det virker kanskje ikke som en stor endring når vi snakker om hundrevis av grader, men det merkes like godt for stålet som du kjenner forskjell på 10 plussgrader og 20 plussgrader.

Ved 910 °C skjer det samme igjen, men denne gangen i revers. Krystallstrukturen går tilbake til BCC. Jernet er ved dette stadiet lyst rødt og er en vanlig temperatur for å smi. Ved 770 °C når vi enda et kritisk punkt, men her skjer det ingen endring i krystallstrukturen. Dette er temperaturen der metallet kan bli magnetisk og dersom atomene i materialet alle vrir seg til å “peke“ samme vei vil jernet bli ferro-magnetisk. Dette punktet kalles Curie-punktet. Over denne temperaturen er atomene i for stor bevegelse til å kunne holde en retning.

Alle disse punktene forekommer i omvendt rekkefølge ved oppvarming og er grunnen til at det kan virke som materialet “holder igjen” litt til tider når det varmes opp. Temperaturene er litt annerledes for oppvarming som for nedkjøling, men stort sett likt.

Mengden karbon i stålet har en tydelig endring på egenskapene og oppførselen til metallet. I flytende form er karbonet i fullstendig løsning i blandingen, og i første omgang ser man at smeltetemperaturen synker.

Når et materiale blir løst opp i et annet kalles det diffusjon. Dette blir i mange tilfeller en homogen blanding, der stoffene er likt fordelt gjennom det hele. En heterogen blanding vil si noe som ikke er fullstendig løst opp og vil ha klumper av ett stoff fordelt i det andre. Også kjent som emulsjon.

På samme måte som det er en metningsgrense for hvor mye sukker du kan ha i kaffen (ikke din metningsgrense kanskje, men for løsningen😉), er det en metningsgrense for mye karbon som lar seg løse opp i jern. Som i eksempelet med kaffe kommer det et punkt der mer sukker ikke lar seg fordele i kaffen og vil samle seg på bunnen. Blandingen har nådd sitt ekvilibrium, det er likevekt. Hva som er metningsgrensen mellom to stoffer avhenger av stoffene. I tilfellet med jern og karbon er det ca 6,67 vektprosent karbon. Disse stoffene er i ekvilibrium ved 4,3 vektprosent.

Hvilke faser og strukturer som eksisterer i stål med ulike mengder karbon ved ulike temperaturer kan leses av i noe som kalles et fasedigram eller ekvilibriums-diagram:

View fullsize

Dette diagrammet har temperatur på Y-aksen og karboninnhold på X-aksen. Det går fra rent jern på venstre side og stopper ved jernkarbid på høyre side. Diagrammet viser ikke noe mer enn det siden det ikke lar seg gjøre å løse opp mer karbon i jernet enn 6,67%. Ytterligere karbon samler seg som klumper av grafitt i blandingen.

Når det er sagt så er mengden karbon som lar seg løse opp i jern avhengig av temperatur og krystallstruktur. Når jern og karbon er i en flytende løsning er det en homogen blanding. Dersom jern og karbon er i ekvilibrium sies det at det er eutektisk.

eu-tekt-isk, (fra gresk eutēktos (smelter lett); eu (bra, godt), tēktos (smelte); punktet der en blanding har et metningsforhold slik at begge substansene smelter og stivner sammen ved en fast temperatur.

Som vi kan se av diagrammet er alt over den øverste streken (ABCD) flytende, denne streken kalles liquidus og siden tilføring av karbon senker smeltetemperaturen til stålet så er streken kurvet nedover mot midten. Dette kommer av at det kreves mer energi å bryte opp større og renere krystaller. Når vi tilfører “urenheter” (i dette tilfellet karbon) så blir det lettere for varmen og “trenge inn“ i jernet og bryte det opp. På andre siden av punktet C der den øverste streken treffer den under, går temperaturen opp igjen til vi når jernkarbid. Streken under dette (AHJEF) kalles solidus, og alt under denne streken er solid.

Punkt C, der de to øverste kurvene møtes, er det eutektiske punktet der blandingen vil stivne sammen og ikke gå gjennom et slush-stadie der en komponent har er annen smeltetemperatur enn den andre, som vises i områdene til høyre og venstre for dette punktet. Alt til venstre for dette punktet sies å være hypo-eutektisk, eller under-smeltende, mens alt til høyre sies å være hyper-eutektisk, altså over-smeltende. Som diagrammet viser regnes alt over 2,06% karbon for å ikke være stål, men støpejern. Mens alt under 0,02% regnes som ferritt og altså mer eller mindre rent jern, med andre ord, ikke stål.

Så hva betyr alle disse ordene?

Ferritt, austenitt, cementitt, martensitt, perlitt, bainitt, ledeburitt og grafitt er navn på ulike faser og mikrostrukturer av kornene i stålet. Disse strukturene brukes for å identifisere og definere ståltyper og egenskaper. Forekomsten av disse avhenger hovedsakelig av tre ting: karboninnhold, varme og nedkjølingstid.

Dette er metallurgiske termer; de relaterer til krystallformer og typer, og atomsammensetningene i disse.

Ferritt (ferrite): Fase og struktur. BCC-struktur. Rent jern. De hvite områdene på bildet er ferritt-korn. Her kan man også tydelig se korngrensene mellom krystallene.

Austenitt (austenite): Fase. FCC-struktur. Oppkalt etter Sir William Austen. En solid løsning av karbon i jern som kun oppstår ved høye temperaturer (en solid løsning vil si et fast materiale med en mindre komponent av et annet stoff spredt uniformt igjennom krystallstrukturen; husk at jernet ved bearbeidstemperaturer regnes fremdeles som solid, bare særdeles mye mykere). Austenitt eksisterer ikke i stål ved romtemperatur. Brukes for å beskrive at jernet har nådd det punktet i oppvarmingen som er nødvendig for at det skal re-krystallisere seg fullstendig, altså det øvre kritiske punktet. Dette punktet avhenger som nevnt av karboninnholdet. Stål sies å være austenittisk hvis det har blitt avkjølt over lang tid og ikke er herdet, selv om strukturene som finnes i dette resulterende stålet ikke direkte heter austenitt. Det er intet kritisk punkt ved 1392 °C i austenitt.

Ledeburitt (ledeburite): Fase og mikrostruktur. En blanding av karbon i jern på 4,3%; en eutektisk miks av austenitt og cementitt. Dette er ikke et stål i seg selv og oppstår vanligvis i høy-karbon stål. Finnes vanligvis sammen med cementitt og perlitt. De svarte feltene i bildet er grafitt omgitt av ledeburitt.

Cementitt (cementite): Fase og mikrostruktur. Jernkarbid (Fe3C), en meget hard mikrostruktur som får sitt navn fra cementeringsprosessen hvor det først ble identifisert. Også noen ganger kalt «keram». Cementitt er en mettet legering som inneholder 6,67% karbon. Jernkrystaller i BCC-struktur kan ikke holde mer karbon enn dette.

Perlitt (pearlite): Mikrostruktur. Perlitt, som får sitt navn fra perlemor, er en blanding av ferritt og cementitt, arrangert i en lamellær (lagvis) struktur. Oppstår ved sakte nedkjøling av austenitt som inneholder over metningsgrensen sin med karbon ved en høyere temperatur.

Martensitt (martensite): Mikrostruktur. Kald og solid austenitt. Selvmotsigende siden jeg nettopp sa at austenitt ikke eksisterer i «fast» form, spesielt ikke avkjølt, men dersom oppvarmet stål bråkjøles (altså herdes) vil det ikke rekke å gå gjennom transformeringen til andre strukturer som cementitt og ferritt og bli fryst fast slik det var, dette kalles da martensitt og er svært skjørt og veldig hardt. Martensitt er det vi prøver å oppnå når vi herder noe.

Bainitt (bainite): Mikrostruktur. Bainitt er en mellomting mellom perlitt og martensitt som oppstår når austenitt blir kjølt ned ved en slik rate at krystallstrukturen rekker å omforme seg, men ikke så raskt at full adskillelse av ferritt og cementitt oppstår. En nålete plate-lignende struktur.

Øvre bainitt

Nedre bainitt

Så, først å fremst er karboninnholdet viktig. Mer karbon gir en sterkere legering. Deretter er varmen viktig, materialet må tilføres nok energi til å løsne på krystallene og la dem omforme seg slik at vi kan oppnå en annen krystallstruktur. Men viktigst av alt i varmebehandlingen er nedkjølingstiden. Eller, karbonet er vel det viktigste, siden jern alene KAN IKKE HERDES, men hvis ikke karbonet behandles riktig er vi jo like langt.

Forholdet mellom temperatur og nedkjølingstid - og resulterende strukturer - finnes i noe som kalles et S-kurve diagram, eller rettere et TTT-diagram (Time-Temperature-Transformation).

View fullsize

“Eutektoid temperature” refererer til det nedre kritiske punktet. Hvis noe er -oid så betyr det av det ligner noe eller er lik, men ikke det samme som noe. Akkurat som primater er humanoider. I dette tilfellet betyr eutektoid at noe omformer seg likt eller samtidig, det er sammstemmelse i materialet, på samme måte som det eutektiske punktet i et smeltebad betyr at fasene er i likevekt og vil stivne sammen. Den eutektoide temperaturen er altså den minste temperaturen vi må oppnå for at krystallstrukturen skal kunne forvandle seg (den nederste rød stiplede linjen på ekvilibriumsdiagrammet), derfor kalles det det nedre kritiske punkt.

Vi kan se at det eutektoide punktet til austenitt, altså metningsgrensen for karbon i austenitt er ca. 0,8% ved den nedre kritiske temperaturen, ca. 723°C. Over denne mengden karbon eller under denne temperaturen, begynner det å fortrenge overflødig karbon ut av blandingen under nedkjølingen som blir til jernkarbid og dermed danner perlitt. Det er over denne mengden karbon man ikke kan oppnå ren perlitt uten å få separate biter av jernkarbid.

Dannelsen av perlitt.

“Austenittisk“ stål. Man kan se at kornene er store og homogene med klare, skarpe og tynne korngrenser.

Denne prosessen tar tid, og det er viktig å la stålet få kjøle ned sakte og la fysikken gjøre jobben sin dersom man prøver å oppnå en slik struktur. Dette kommer klart frem av diagrammet, der A er austenitt, P er perlitt, B er bainitt og M er martensitt. Som vi også kan se så begynner ikke omformingen av austenitt til martensitt før ved ca 220°C og slutter når blandingen når litt over 100 grader (Den avslutter egentlig aldri, men for praktiske årsaker sier vi at den gjør det). Hvis vi trekker en strek fra den eutektoide temperaturen ved 0 sekunder, ned til herdebadets temperatur ved f.eks. 10 s, ser vi at den hadde gått forbi de andre fasene og gått rett fra austenitt til martensitt. Dersom stålet hadde brukt litt lenger tid, hadde vi sett spor av perlitt og til slutt bainitt når det når grensen for martensitt siden det har rukket å gå inn i “S-kurven“, og bruker det enda lenger tid ender vi opp med et mykt austenittisk stål av eventuelt perlitt eller lederburitt, avhenging av karboninnholdet.

Så lenge stålet er austenittisk når det når grensen for martensitt vil det omforme seg til dette. Det er stort sett kun avhenging av tid, gitt at den nødvendige fasen er tilstede. Martensitt er stort sett det som menes om når det snakkes om herdet stål. Austenitten er som sagt i en FCC -struktur, men ved høyere temperatur (over det øvre kritiske punktet, ca 910°C) vil ferritten være BCC og ha plass til en god del karbon.

Så, når vi har en en varm bit med stål med veldig spredte atomer som har mye plass mellom seg, er det plass til karbonatomer, som er mindre enn jernatomer, til å trenge seg inn i selve krystallstrukturene i kornene. Når vi samtidig har en rask nedkjøling som skaper små korn, og nok karbon til å lage sterke korngrenser, kombinert med de nevnte sprekkferdige krystallene som blir låst fast med karbonet fordi det ikke har tid til å bli fortrengt…

Da får vi et martensittisk stål. Det er knallhardt, men ekstremt skjørt.

I neste innlegg om stålets fantastiske egenskaper skal vi ta for oss mer praktiske eksempler og metoder, og betydningen av herding (som du nå forhåpentligvis har en bedre teoretisk forståelse av), anløping, normalisering, utgløding, settherding, flammeherding og annet spennende stoff som faktisk har en praktisk verdi.

For å oppsummere: Karboninnholdet i jernet har innflytelse på hovedsakelig 3 egenskaper: hardhet, formbarhet og bruddstyrke.

Og: Disse egenskapene kan vi endre med 2 variabler: temperatur og tid.

View fullsize

Dette innlegget var tungt å skrive og krevde mye research. Dersom du kan mer om dette enn meg og oppdager noe som er feil, skriv en kommentar eller kontakt meg på mail så jeg kan få rettet det opp. Det er mulig jeg tar en pause fra å skrive om stål og skriver om noe litt lettere stoff fremover, men det siste innlegget kommer (og kanskje et bonusinnlegg, det er hemmelig inntil videre). Takk for at du leste, og håper det kommer til nytte.

Justering av avtrekk på flintlås

Det er en stund siden siste innlegg her, men jeg har vært i en periode med mye endringer; jeg har flyttet og begynt i ny jobb. Loggen fortsetter, dog med et lavere tempo. Jeg har noen interessante innlegg kommende etterhvert, men de tar tid å skrive. Nok om det.

View fullsize

Jeg fikk anledning til å jobbe med et pekuliært våpen nylig; en 1700-talls flintlås pistol! For de som ikke vet hva det er, er flintlås et begrep som omfatter mange ulike våpen som benytter en avfyringsmekanisme der flintstein brukes for å antenne kruttladningen. Oppfunnet ca. 1600 — en etterkommer av snapplåsen og hjullåsen — og benyttet i stor grad frem til tidlig 1800 da perkusjonslåsen gjorde sitt inntog.

View fullsize

Brukt hovedsakelig på musketter og andre glattløpede munnladere, som denne, naturligvis kortere, pistolen. Tidlig kruttvåpenteknologi gikk ut på å utvikle raskere, enklere og mer pålitelige måter å antenne en kruttladning utenfor våpenets kammer, som så brant som en lunte inn i våpenet og antente hovedladningen. I motsetning til perkusjonslåsen, som var det første store steget vekk fra denne måten å antenne ladningen på, var flintlåsen relativt treg i funksjonen. Med tanke på at kruttet skulle ta fyr og brenne inn i kammeret så kunne dette under dårlige forhold ta opp til ett sekund mellom avtrekk og avfyring, men på en godt laget flintlås kunne denne forsinkelsen være umerkelig.

View fullsize

Litt krutt helles i fengpannen og det fjærbelastede fengstålet lukkes over for å holde kruttet på plass og beskyttet fra vær og vind. Når avtrekkeren trekkes slippes hanen, som har en bit med flint låst fast i en tvinge-lignende anordning, og slår mot fengstålet slik at det åpner seg og samtidig produserer gnister som blir rettet mot kruttet i pannen. Dette antenner og brenner inn til hovedladningen gjennom et hull i siden av kammeret.

Problemet med denne spesifikke pistolen var at den ikke avfyrte; man kunne spenne hanen bakover, men et trekk i pang-spaken førte ikke til hanefall.

Det kan ha ymse forklaringer, f.eks. at overføringen fra avtrekker til avtrekkerhake er ødelagt, eller at inngrepsflatene er slitt eller ødelagt og henger seg opp. Det var sistnevnte som var problemet her.

View fullsize

Ikke avbildet her er slagfjæren som er en bladfjær som ligger langsmed platen og presser ned på utstikkeren fra spennstykket — som jeg også lærte heter “studdel“. Norske navn på våpendeler er så søte.

View fullsize

Det er to hakk på studdelen, det første er halvspenn og er formet mer som en krok slik at det skal være umulig å trekke av når avtrekkerhaken er i inngrep med denne. Denne posisjonen brukes når våpenet skal lades og hanen må fjernes fra kruttpannen for fylle på krutt. Den andre er inngrepsflaten for avtrekkerhaken og er den som haken trekkes ut av for å avfyre våpenet.

Inngrepsvinkelen er viktig og bidrar mye til hvor sikkert våpenet er og hvor godt avtrekket er. Dersom vi har negativt inngrep kan slagfjæren alene ha kraft nok til å dytte avtrekkerhaken ut av inngrep og våpenet kan gå av av seg selv, også kjent som “hair trigger“, der det bare skal til at du ser hardt på avtrekkeren før det smeller. Dette er ikke ønskelig og er veldig farlig.

View fullsize

Nøytralt inngrep er stort sett helt akseptabelt, der spennkreftene går vinkelrett gjennom inngrepsflatene. Problemet med dette er at dersom avtrekkeren trykkes litt inn og slippes igjen vil ikke inngrepsflatene dytte hverandre på plass igjen og våpenet er nå litt mindre sikkert enn det var. Det er derfor lurt å ha en lett positiv inngrepsvinkel slik at dersom avtrekkeren trykkes inn og slippes igjen vil slagfjæren og avtrekkerhakens fjær sammen dytte inngrepet tilbake til normal posisjon. Dette vil riktignok skape et tyngre avtrekk og er grunnen til at hanen beveger seg ørlite gran bakeover ved avtrekk før den faller. På konkurransevåpen er det vanlig med et mer nøytralt inngrep, mens på militære våpen er inngrepet tungt positivt av sikkerhetsårsaker.

Inngrepsflatenes individuelle vinkel i forhold til deres respektive vippepunkt er også av betydning. Det er ønskelig å ha hanens inngrepsflate på linje med vippepunktet for å minimere hanens bevegelse i avtrekket. Avtrekkerhakens inngrepsflate bør være tangensiell hakens vippepunkt og kan justeres ved å endre vippepunktet.

View fullsize

Det er også viktig at inngrepsflatene matcher slik at belastningen i systemet fordeles over en flate og ikke hviler på ett punkt av avtrekkerhaken. Dette fører til voldsom slitasje og kan ødelegge tuppen av avtrekkerhaken slik at avtrekket blir ruskete og uforutsigbart. Det er også selvsagt viktig at kantene på inngrepsflatene er parallelle slik at belastningen ikke hviler på kun venstre eller kun høyre side av avtrekkerhaken.

Så hvordan fikser vi dette? Hanens inngrepsflate var ikke flat men hadde en lett konkav form og avtrekkerhaken var ikke flat og skarp.

View fullsize

Siden disse delene skal tåle mye last på et lite punkt og ikke deformeres er de herdet knallharde, så filing er bare å glemme. Vi må ty til abrasjon. Abrasive verktøy som diamantfiler eller steinbryner gjør susen. Det er også viktig å ha en god guide til slipingen for at flatene skal bli parallelle og flate igjen. Dette er ikke noe som gjøres for hånd uten oppspenning. En herdet stikke som tåler det verktøyet vi vil gni over den er nødvendig.

View fullsize

Delene settes i mekanismen og en inngrepsvinkel observeres eller bestemmes og på best mulig måte tegnes eller på annet vis lages for å se vinkelen vi skal påføre delen når den står i stikken. Deretter slipes flaten parallelt med toppen på stikken. Her er det viktig å la verktøyet gjøre jobben og ikke påføre for mye trykk. Det finnes andre måter å gjøre dette på, det viktigste er bare at vinkelen holdes konsekvent.

Når det er sagt så er ikke flintlåsmekaniskmer fra sent 1700 tall høyden av mekanisk presisjon, så det var ikke mye som skulle til for å få den til å fungere igjen, men det var interessant å dissekere den.

Timing av gjenger

Timing av gjenger kan være nødvendig i mange forskjellige situasjoner der to deler som skrus sammen må stå i en viss vinkel i forhold til hverandre.

Her skal en del som skrus på passe slik at A og B havner på linje, men delen stopper ved punkt C. Hvordan løser vi dette?

Som et eksempel er det viktig for rekylbremser på rifler, som må stå rett slik at gassene blir omdirigert korrekt.

Det er selvsagt mange andre scenarioer der timing er nødvendig, men som et eksempel, la oss bruke det ovennevnte tilfellet siden det ligger naturlig for meg å bruke det.

Det finnes flere metoder å sikre at to deler som sammenføyes med gjenger times korrekt:

Hvis noen av disse må brukes så er shims eller laminatskive det beste alternativet ettersom de fungerer som en forlenging av brystningsflaten og opprettholder parallellitet og konsentrisitet bedre enn crush-skive og kontramutter, som begger er ganske dårlige alternativer.

Men alt handler jo til syvende og sist om brystningsflaten, og det aller beste er at de to delene som skal skrus sammen møtes direkte på denne. Da er det aller beste alternativet for å time delen at brystningsflaten tilpasses. Dette er litt mer innviklet, men ikke vanskelig.

En ren brystningsflate som er i rett vinkel til gjengenes akse er nødvendig. Denne flyttes bakover ved å fjerne litt materiale slik at delen som skrus på kan skrus lenger inn og dermed havner i en annen vinkel enn før.

Hvis vi har en stigning på 1 mm og vi fjerner 1 mm av brystningsflaten så vil delen som skrus på havne i samme vinkel, bare 1 mm lenger bak. Så for å endre 1° må vi fjerne 1/360 del av stigningen.

Men hvordan finner vi ut av hvor mye som skal fjernes?

Så for å flytte Tp til Tf må vi fjerne B, og for å finne den er det er par ting vi må vite:

• Avstanden mellom ønsket stopp-punkt og nåværende stopp-punkt (ΔT)

• Omkretsen av den delen vi skal flytte brystningsflaten på (C)

• Stigningen (P)

For å finne ΔT kan vi legge en teip-bit rundt og markere Tf og Tc og måle avstanden. Det finnes andre mer nøyaktige metoder, og man kan også regne seg frem til det hvis man vet vinkelen, men da trenger man ikke denne metoden.

Deretter kan vi regne ut hvor stor del av den totale omkretsen C som ΔT utgjør. Vi kan kalle dette forholdet for Ct:

Deretter kan vi bruke dette forholdet Ct til å finne ut hvor mye av stigningen P dette utgjør:

Altså blir hele formelen:

Det går selvsagt også an å oppnå det samme resultatet ved å endre på brystningspunktet på den delen som skrus på.

Det er lurt å ta av litt mindre enn det man regner ut ettersom noe av timingen kan gjøres vel tilstramming og man har litt å gå på ettersom hvor hardt man strammer.

Ved èn veis ende

Atter et skoleår er over. Det siste jeg behøvde. Det har vært en lang reise til dit jeg er kommet hittil, og veien videre til svennebrev som børsemaker er fortsatt lang, men jeg er meget godt på vei nå. Jeg har fått lærlingplass, men den er opptatt i et år til, så jeg skal jobbe litt mens jeg venter.

Denne loggen har vært en kilde til både inspirasjon og frustrasjon, men den har uten tvil hjulpet meg godt på veien dit jeg ville. Siden den hovedsakelig fungerte som en skolelogg har den nå utført sin oppgave og er strengt tatt ikke nødvendig mer, men jeg er blitt svært glad i den, og den inneholder mye nyttig informasjon, både for meg selv og forhåpentligvis andre, så den kommer ikke til å gå noe sted med det første.

Jeg kommer nok til å fortsette å skrive innlegg her, men frekvensen vil nok gå litt ned. Det vil trolig komme litt mer innlegg igjen når jeg begynner lærlingtiden min i 2019.

Til slutt vil jeg takke alle som har hjulpet meg å nå dette punktet, dere vet hvem dere er. Og takk til alle mine medelever dette skoleåret i Støren, det har vært et fantastisk år og jeg er glad for at jeg ble kjent med dere. Og ikke minst takk til skolen og lærerne som ga meg en sjanse og trodde på meg, jeg har lært mye av dere og jeg tror kanskje dere har lært litt av meg også! 

Takk.