Sinus, cosinus og tangens
/Det må være et universalt faktum at vi mennesker hater å bli påtvunget lærdom vi ikke ser nytten av. Dersom noe ikke interesserer oss er det verdens største motbakke å lære seg det. I samme grad tror jeg ikke det finnes det menneske som ikke på ett eller annet tidspunkt har yttret “når kommer jeg til å få bruk for dette?“ .
Det er interessant hvordan hva som definerer den grunnleggende skolegangen til stadighet øker i kompleksitet og omfang. En grunnskoleutdannelse er mer omfattende i dag enn den var for 100 år siden. Og med god grunn, siden den sosiale og teknologiske forståelsen som kreves for å fungere i dagens samfunn er langt større enn den gang. Vi vet mer nå enn vi gjorde da, og derfor tar det lenger tid å få folk “up to speed“ på dagens verdensbilde. At dagens skolesystem er totalt uegnet for den oppgaven er et annet kapittel, der dens primære oppgave fortsetter å være en utdatert doktrine for å masseprodusere akkurat-passe-kompetente fabrikkarbeidere, i denne digitale tidsalder og automasjonsrevolusjon, er en synd og en skam, men det er nå en gang slik det er inntil videre.
Når skal man sette grensen for hva som kreves av kunnskap hos et menneske som skal ha en grunnleggende forståelse for verden, og et godt grunnlag for videre spisskompetanse? Det er et godt spørsmål. Hva er grunnivået? Burde vi begynne å spesialisere oss tidligere?
Ingen kan vite alt om alt, men alle kan vite det meste om noe, og alle burde vite litt om det meste.
Vi har riktignok begynt å bevege oss i riktig retning, men det er fremdeles en lang vei å gå.
Det viktigste skolen kan lære en elev er kunsten å tilegne seg kunnskap selv.
Hvor relatert paragrafen over er til det jeg egentlig vil skrive om er jo en diskusjon i seg selv, men jeg ble inspirert til å skrive om dette siden det er noe jeg selv ikke forsto ordentlig før lenge etter min skolegang var avsluttet, og det skremte meg. Det er vel ikke alt for langt å strekke seg å si at alle har eller har hatt en aversjon for matematikk i en eller annen grad. Som det opprinnelige poenget mitt ga, “når kommer jeg til å få bruk for dette?” er et helt legitimt spørsmål, og spør du meg så er det ikke nødvendig at en trenger å lære å løse komplekse ligninger på videregående dersom en ikke skal ta høyere utdanning innen fagfelt som har behov for å kunne det, som fysiker eller matematiker. Når det er sagt så må jeg jo til skolesystemets forsvar si at det er jo heller ikke sånn; det finnes grader av matematikk basert på hvilket utdanningsløp man tar, så noe av det jeg etterspør eksisterer allerede, og mye av mine meninger er nok smurt med et tykt lag av subjektive oppfatninger som bunner i skoletretthet fra første gang jeg gikk på videregående. Men hvorfor ble jeg lei av skolen i utgangspunktet er poenget mitt? Visste jeg ikke hva jeg gikk til? Var jeg bare ung og dum? Eller var det et dypere problem med systemet?
Uansett hva årsaken måtte være, så har jeg nå endt opp som hovedsakelig maskinist og metallarbeider, som ifølge dagens skolesystem behøver noe som heter praktisk matte. Hvilket går ut på mer praktisk orientert matematikk som geometri og prosentregning og denslags, og ikke så mye fokus på algebra og sannsynlighet og slikt.
Hvilket er greit nok, et steg i riktig retning som sagt, og grunnlaget for dette innlegget er egentlig ikke frustrasjon over innholdet i utdanningen, men læringen av det. Jeg kan selvsagt ikke snakke for alle, og lærere har min ytterste respekt, (spesielt på videregående nivå der de må forholde seg til et veldig slitsomt stadie av et menneskes utvikling, folk burde egentlig ikke begynt på videregående i en alder av 16 spør du meg), men jeg spurte alltid om hvorfor ting er som de er, hva er grunnen til at det og det blir det, hva er årsaken til at det er slik, hvem fant det opp, hvorfor, hva brukes det til, etc. Hvilket jeg svært sjeldent følte jeg fikk et tilfredsstillende svar på. Og nå som jeg endelig har fått svar på det jeg den gang lurte på gir alt så mye mer mening, og min forståelse for subjektet er mye, mye større.
Men det er det som plager meg. Jeg fikk aldri forklart hvorfor noe er som det er. Jeg ble fortalt at slik er det og det må du pugge og kunne. Hvorfor jeg måtte pugge og kunne er igjen et spørsmål som kan rettes til mitt første paragraf, men lære det måtte jeg. Og å lære noe uten å forstå hvordan det fungerer eller hvorfor man må lære det er ikke bare ødeleggende for selvtilliten til eleven, det er også utmattende.
Så i lys av mine egne erfaringer med skolesystemet og nye forståelse for et felt som er av ypperste viktighet for folk i mitt yrke, her er mitt forsøk på å forklare trigonometri:
Av alle matematiske felt må geometri og trigonometri være de aller mest interessante for meg. Kunnskap man faktisk ofte har bruk for, og kan benytte praktisk på mange områder. Ordentlig forståelse av trigonometri får en til å se helt annerledes på verden.
Ordet TRIGONOMETRI kommer, som så mye annet, fra gresk, og betyr trekantmåling. Det er alt trigonometri handler om. Måling og beregning av trekanter.
Det handler i all hovedsak om å finne vinkler når vi vet lengder på sider, og vice versa. To dimensjoner som ikke nødvendigvis er direkte intuitivt sammenkoblet.
Så når man virkelig forstår trigonometri og forholdene det omhandler finner man så mye mer glede i å bruke det.
I all hovedsak er det de esoteriske matematiske funksjonene ved navn sinus, cosinus og tangens jeg vil snakke om. Det er mye annet som også er viktig å kunne innen trigonometri, mest grunnleggende Pytagoras læresetning, men også bl.a. sinus-setningen og cosinus-setningen (law of sine/cosine) for utregning av ting i ikke-rettvinklede trekanter, men hvis jeg skulle prøvd å forklare det kunne jeg blitt her en stund. Men disse litt mer avanserte formlene bunner i å gjøre om andre trekanter til rettvinklede trekanter for å regne dem ut, så det er vel ikke feil å si at all trigonometri stammer fra den rettvinklede trekanten. Priset være den.
Så la oss holde oss til rettvinklede trekanter. Litt kvikk oppfriskning;
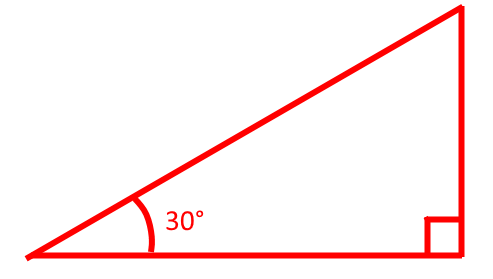
En rettvinklet trekant er en hvilken som helst trekant der én av vinklene er 90°:
Firkanten i høyre hjørne betyr at denne vinkelen er 90°. Vinklene i en trekant blir alltid til sammen 180°. Dette gjelder alle trekanter. Det kan bevises på ulike måter, men hvis du forestiller deg at den nederste streken ble kortere og kortere, og den vinkelen som er 30° kom nærmere og nærmere den høyre siden av trekanten, ville den gradvis også nærme seg 90°, helt til du ender opp med 2 streker som går rett opp og ned, og ligger oppå hverandre som begge er “90°“. 2x90=180. Tada.
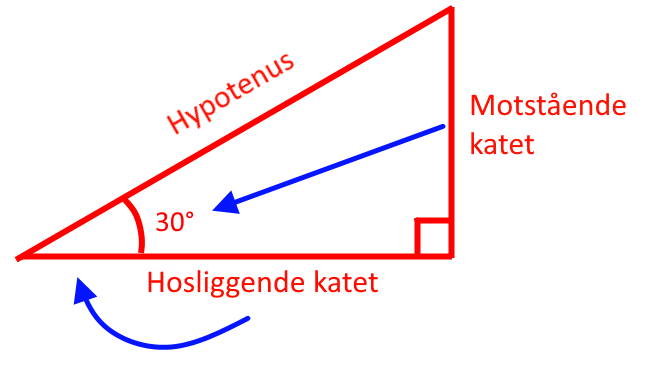
Den lengste siden er Hypotenusen. Hypotenus kommer fra latin og gresk og betyr “strukket under“, hypo- (under) og ten- (strekke, som i eng. tensile strength).
Spør meg ikke hva det liksom er meningen at den skulle være strukket under, men jeg tenker at det er ment mer abstrakt enn bokstavelig, i den forstand at den er strukket mellom to punkter under forholdene eller kunnskap om hva disse strekene er, eller noe i den duren.
De to andre sidene som sammen utgjør 90°-hjørnet er Katetene. De kan navngis ytterligere, basert på hvor vinkelen vi snakker om ligger. I tilfellet over vil den nederste linjen hete “hosliggende katet” (eng. adjacent side) og den høyre linjen vil hete “motstående katet“ (eng. opposite side).
Navngivningen er nokså selvforklart, den motstående katet er den som vinkelen “peker på“, så hadde vinkelen vi snakket om vært den oppe til høyre ville navnene vært motsatt. Dette er viktig senere.
Hva er egentlig en vinkel og hvorfor er 90° rett?
Hvorfor bruker vi 360°? Vel, det er mange måter å uttrykke vinkel på, det er mer eller mindre tilfeldig at vi bruker grader mest. En sirkel er delt opp i 360 grader, men det er ikke noe iboende sammenheng mellom sirkler og tallet 360. Vi kunne like gjerne brukt 1000 eller 548, men sistnevnte høres ikke spesielt enkelt ut å regne med. Grunnen til at vi bruker 360 er av samme grunn som minutter og timer er delt inn i 60, det er flere faktorer for disse tallene enn mer runde tall i 10-tallsystemet.
360 har 24 faktorer: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, 360
400 for eksempel har bare 15: 1,2,4,5,8,10,16,20,25,40,50,80,100,200,400
Da det metriske system var under utvikling i Frankrike på 1700-tallet var det et forsøk på å flytte over til å regne med 400 grader, slik at en rett vinkel ble 100°, men det var ikke noen suksess, p.g.a. poenget over. Men dette er faktisk i noe bruk i dag og heter en gradian.
Kanskje vi burde delt inn en sirkel i 5040? Det tallet har hele 60 faktorer!
Men det finnes en enda bedre, mer matematisk sammenhengende måte å uttrykke vinkler på: Radianer
Hvorfor tar jeg opp dette? For å virkelig forstå sinus og kompani må vi vite om radianer.
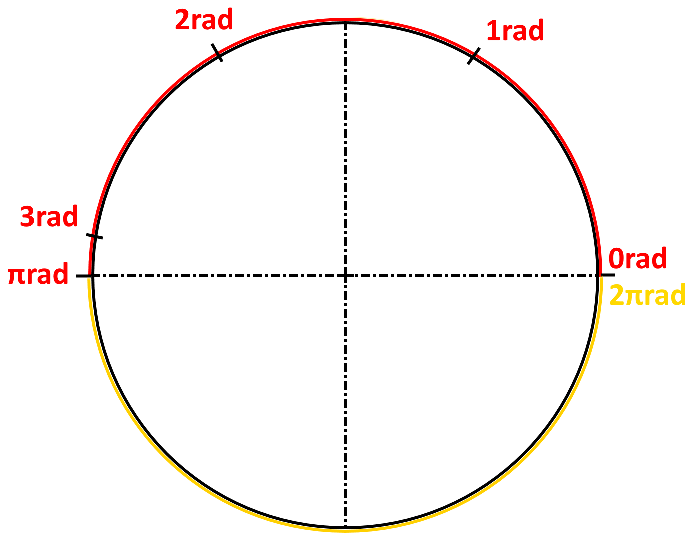
Radianer er en måte å uttrykke vinkler på med radien til en sirkel. Størrelsen på denne sirkelen er likegyldig, siden det er er forhold vil det alltid stemme. Omkretsen av en sirkel er som kjent 2πr, så 180 grader av en sirkel langs sirkelen blir π ganger radien. Hvis vi kunne uttrykt vinkelen som en del av denne omkretsen så kan vi si at vinkelen er en andel av π ganget med radien. Hvis vi pakker radien rundt sirkelen langs omkretsen slik:
Da får vi 1 radian. 1 radian tilsvarer 57.2957795°, hvilket ikke er så brukervennlig i dagligtale.
90° blir rundt 1.57 rad. 3 rad blir nesten 180°. 180 grader er 3,1415 rad, altså πrad. 360° blir altså 2πrad.
Så hvis radien er 1 blir en hel omkrets 6,28…..etc. Derav 2πr. Eller πd om du vil. Eller τr om du føler deg ekstra dristig.
Her er en fin animasjon som illustrerer det godt, hentet fra Wikipedia:
Radianer er altså en renere, direkte sammenhengende, matematisk uttrykkelse av vinkel. Når du regner ut grader på kalkulatoren så regner den med radianer og omgjør det til grader som vi er mer vant til og lettere for oss å lese. Dersom du setter kalkulatoren til å vise rad så ser du svaret i rad, hvilket har forvirret meg ved flere anledninger der jeg ikke så at den var stilt til rad og ikke deg (degree). De fleste formler som omhandler vinkler og slikt på akademisk nivå bruker radianer.
Omgjøringen av radianer til grader er:
Siden π rad tilsvarer 180° så deler vi opp π i 180 (som blir ca. 0.017 ) og ganger med hvor mange grader vi hadde i vinkelen vår, så får vi hvor mye av π det tilsvarer.
Likedan, når vi gjør om fra rad til deg, så må vi dele opp 180 i π deler (som blir ca. 57,3) og så gange med hvor mange rad vi hadde.
Dersom franskmennene fikk det som de ville og gradianer (400° i en sirkel) hadde blitt standard, ville formelen sett helt lik ut, bare med 200 istedenfor 180.
Så hva har dette med sinus, cosinus og tangens å gjøre?
Vel, kun som bistand til å forstå hvordan de funker. Sinus, cosinus og tangens er funksjoner, mer bestemt trigonometriske funksjoner, mye på samme måte som de mer alminnelige aritmetiske funksjonene som pluss, minus, gange og dele, men de er en del mer komplekse.
Hvordan sinus og cosinus faktisk kalkuleres “bak teppet“, er avansert. Men det er ingen standard måte og regne det ut på, ulike algoritmer eksisterer for å approksimere resultatet av funksjonen. Noe som heter Taylor-serien kan brukes for å beregne en kurve som ligner så mye på en sinuskurve som mulig, mer om det senere.
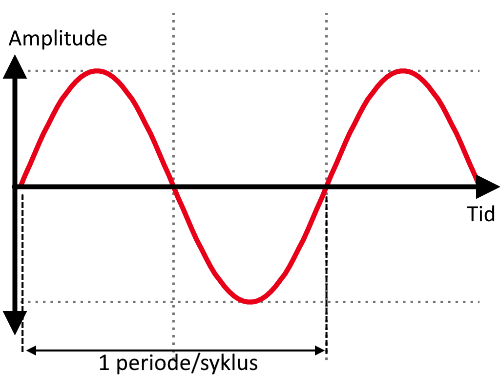
En sinuskurve er spesiell fordi den beskriver en perfekt periodisk bevegelse. En periodisk bevegelse er som man kan tenke seg noe som gjentar seg om igjen og om igjen i et likt mønster over tid:
Eksempelet over er ikke en perfekt sinuskurve (eng. sine wave), men en sinusoid. Som vi lærte i innlegget om stål, så er noe som er -oid noe som ligner på noe, men ikke er det eksakt. Men de kalles gjerne sinuskurver uansett. Men hvorfor ser de sånn ut? Handlet ikke dette om trekanter? Joda. Men kurven er en graf av sinusfunksjonen, så for å forstå funksjonen må vi forstå grafen, og for å forstå grafen må vi se på forholdene i trekanten.
Hva er disse forholdene og hva betyr de?
Nå kommer vi egentlig til selve hjertet av temaet. Forholdene mellom sidene i en rettvinklet trekant. La oss gå tilbake til den første trekanten vår:
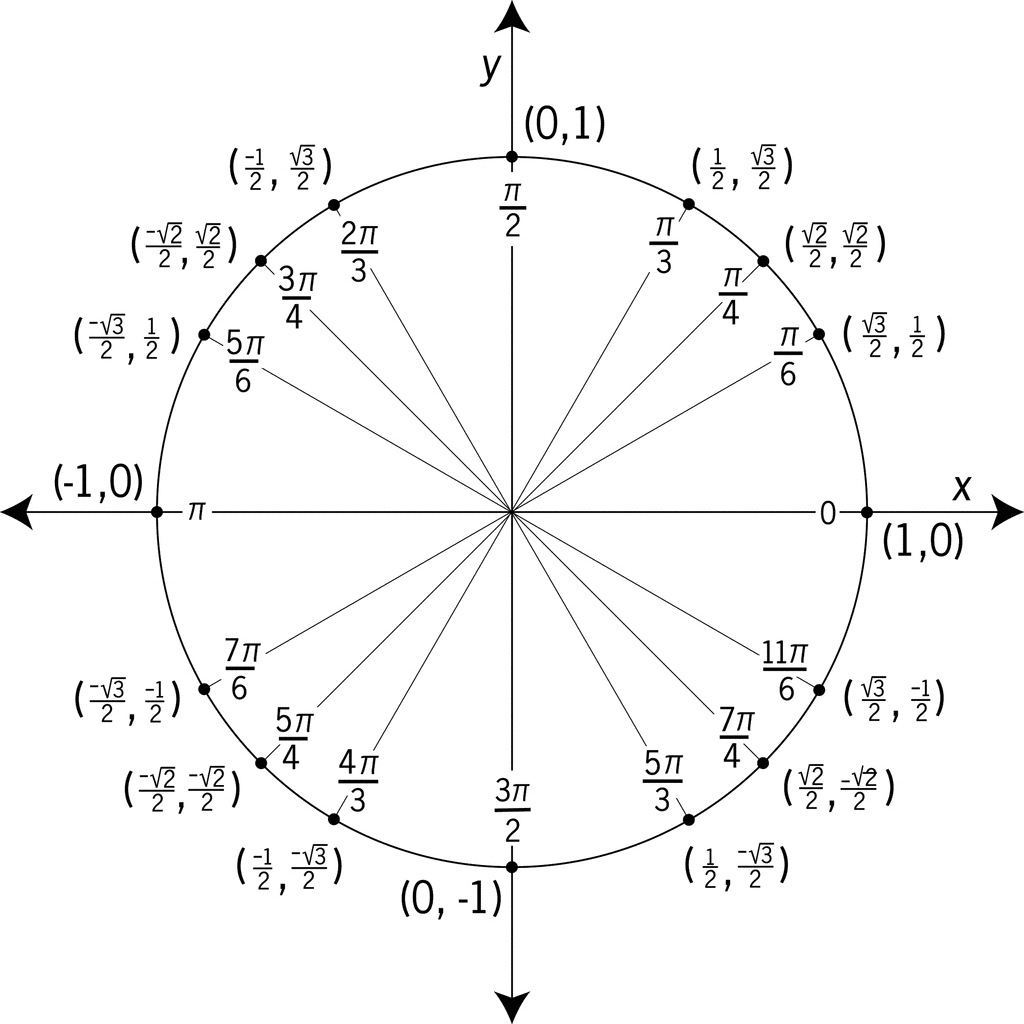
I eksempelet over er θ (theta) 30°. Sinus til 30° er 0,5. Hva betyr det? Det er lettere å visualisere hvis vi putter trekanten inn i noe som kalles enhetssirkelen, en sirkel med radie 1, med senter i origo.
Til høyre er et eksempel på en klassisk representasjon av enhetssirkelen.
Den viser 3 vinkler innen hver kvadrant, samt kardinal-retningene, i radianer i form av deler av pi.
Tallene i parentes viser koordinatene til det punktet uttrykket i fraksjoner av radien.
Vi skal forholde oss til en litt enklere utgave:
Alle strekene som går ut av senter i kardinal-retningene tilsvarer radien, akkurat som hypotenusen i trekanten, altså linje C.
Lengden av linje A og linje B er avhengig av vinkelen θ.
Men hva BETYR dette tallet?
Det betyr at ved en gitt vinkel er den gjeldende katet like lang som hypotenusen ganget med sinus/cosinus til vinkelen.
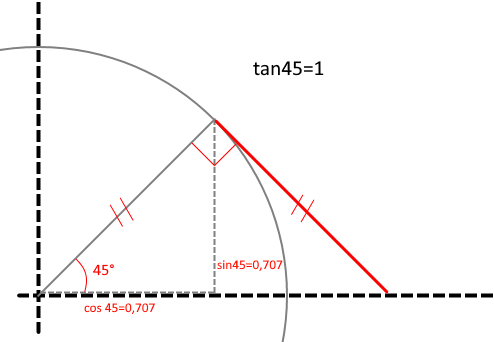
Sinus gir lengden til den vertikale streken i trekanten basert på vinkelen. Når vinkelen er 30° ser vi at den er like lang som halvparten av hypotenusen, altså radien, altså er den 0,5.
Vi kan bevise det visuelt at sin30 = 0,5:
Sinus til 45° er 0,707… Sinus til 60° er 0,866… Og så videre. Jo nærmere vinkelen nærmer seg 90° jo nærmere vil sinus til vinkelen bli 1.
Så hvis vi plotter inn flere punkter ser vi at det begynner å danne en sinuskurve:
Klikk på bildet for å se en større versjon
De røde horisontale strekene til høyre i visualiseringen over er lengden på kurven fra (1,0) opp til det punktet langs omkretsen av sirkelen. På den måten blir en sirkel om til en rar bølge.
Resten av kurven er bare ekstrapolert ut av flere tenkte punkter langs resten av sirkelen. Vi ser at i neste kvadrant vil Y fortsette å være positiv, men X går mot null og vil bli negativ, derav den nedadgående kurven, og når Y blir negativ i de to neste kvadrantene vil sinuskurven dukke under på samme måte. Men den totale avstanden fra start langs sirkelens omkrets fortsetter å øke, derfor fortsetter bølgen stadig til høyre.
Her er en bedre visualisering, også hentet fra Wikipedia:
Over ser vi en representasjon av en perfekt sinuskurve som følger enhetssirkelen.
Den blå streken er et punkt som beveger seg langs omkretsen. Hvis vi trekker en strek fra origo (senter av sirkelen) til dette punktet får vi en strek med lengde r, altså 1 i dette tilfellet. Ettersom den blå streken beveger seg langs omkretsen øker vinkelen til denne streken i forhold til x-aksen. Hvis vi så trekker en strek fra det blå punktet ned til x-aksen, så vil dette representere “høyden“ til punktet langs y-aksen til enhver tid. Hvis vi følger den gule vertikale streken fra den blå streken og til den røde i grafen, så ser vi hvordan denne “høyden” representeres av den røde streken ettersom det blå punktet traverserer omkretsen. Dette er sinuskurven.
Her ser vi tydelig forholdet til radianer også; en halv π blir rett opp, altså 90°, sinus til 90 er altså 1, og hvis vi prøver det på kalkulatoren ser vi at det stemmer.
Hvis vi plotter det inn i et koordinatsystem vil vi se at amplituden (Y) til kurven som følger enhetssirkelen alltid går mellom 1 og -1, og fullfører en syklus når X=2π
De trigonometriske funksjonene er også ikke-lineære, som vil si at du vil få det samme svaret selv om du øker tallet, så lenge vinkelen som dannes er den samme i forhold til aksene.
Sinus fortsetter å være 0,5 for alle vinkler som skaper den samme lengden på den motstående katet:
f(x)=sinx
Som vi ser på grafen så kan forholdet bare være et tall mellom -1 og 1. Noe over eller under dette vil gi en feilmelding ved bruk av sin eller cos.
På samme måte vil SIN 390, altså en rotasjon + 30°, også bli 0,5.
Dette forklarer sinus, men hva er cosinus?
Hvis sinus er “høyden“ så er cosinus “bredden“. Cosinus definerer lengden på streken som danner “grunnlinjen” i trekanten vår. Altså den hosliggende katet. I motsetning til sinus som definerer den motstående katet. For å si det på en annen måte; koordinatene til punktet som dannes der hypotenusen treffer den tenkte sirkelen kan representeres i X og Y med cosθ og sinθ respektivt, der θ er vinkelen vår.
Vi kan se på bildet under hvordan forholdene mellom sidene i trekantene og vinkelen spiller sammen, og hvordan man kan tenke seg at de relaterer til en sirkel.
Cosinus er 90° “offset” sinus og danner en kurve som starter høyt men ellers er uadskillelig fra en sinuskurve, men den er en kvart syklus asynkron.
Hvil øynene dine på atter en fantastisk visualisering fra Wikipedia:
OK, det er funksjoner, så hva betyr de og hvordan brukes de?
Etymologien til ordet “Sinus“ er lang og knotete, men det kommer fra latin og betyr “favn“ “havn“ eller “bukt“, som er en mistolkning via arabisk og har sitt opphav fra sanskrit “jiva“ som betyr “korde“, hvilket i matematikk er et linjestykke som går mellom to punkter på en kurve (BX).
Cosinus er satt sammen av to deler; rot-ordet “sinus” med prefixen “co“, som betyr “sammen“ eller “motpart“.
Som vi skjønner av dette så er det motsatsen til sinus på en måte, de er alltid i samspill.
Tangens kommer fra Latin fra ordet “tangere“ som betyr “å ta på” eller “berøre“, som i det engelske ordet “tangible“.
Tangens er forholdet mellom de to katetene. Dette vil gi mer mening senere, men du har sikkert hørt ordet “tangensielt“, som i relasjon til sirkler vil si en strek som går ut fra omkretsen på en slik måte at den alltid er 90° i forhold til radien (venstre), eller mer matematisk korrekt er vel å si at det er en strek som går gjennom to uendelig nære punkter på en kurve (høyre):
BX er en korde (eng: chord)
Hvis et objekt blir slynget ut fra en sirkulær bane vil det alltid skje tangensielt.
Tangensen til en graf kan beskrive kurvens vekstrate i det punktet.
Sinus, cosinus og tangens representerer hver for seg forholdet mellom 2 sider i en trekant.
Hvilke 2 sider som forholdet beregnes fra bestemmer hvilken funksjon som er relevant.
Vi har hovedsakelig 9 trigonometriske funksjoner;
Forkortelsene sin, cos og tan er åpenbare og gir deg forholdet til en side ved en gitt vinkel.
Arcsin, arccos og arctan er forkortelser for “arcus sinus“, etc. Arcus betyr “kurve” eller “bue“ og gir deg vinkelen ved et gitt forhold.
Csc, sec og cot er forkortelse for cosekant, sekant og cotangent, respektivt og er det omvendte av sin, cos og tan (csc x = 1/sin x). Disse brukes ganske lite og kan ignoreres.
Arcsin, etc. forkortes ofte til asin, acos og atan, spesielt i programmering.
Matematisk skrives de inverse som oftest:
-1 i dette tilfellet betyr ikke at de er opphøyd i minus 1, men at de er de inverse funksjonene.
Hva er forskjellene på disse og hvorfor er de viktige?
De normale funksjonene lar oss kalkulere sider når vi vet vinkler
De inverse funksjonene lar oss kalkulere vinkler når vi vet sider
Men for å bruke disse funksjonene trenger vi å vite forholdene mellom sidene.
Og hvordan vet vi hvilken funksjon vi skal bruke når?
Vel, hvis vi tenker oss at trekanten vi jobber med står i enhetssirkelen som i eksemplene over, så gir det fort mening.
Men på engelsk har de en fin huskeregel som heter “SOHCAHTOA“.
Denne regla kan deles opp i tre; SOH, CAH og TOA. Den benyttes for å huske hvilken trigonometrisk funksjon som skal brukes avhenging av hva vi vet og hva vi skal finne.
Den første bokstaven i hver del beskriver hvilken funksjon som skal brukes (ord som følger er på engelsk): Sine SOH, Cosine CAH og Tangent TOA.
De andre bokstavene representerer Opposite, Adjacent og Hypotenuse.
Den første bokstaven etter funksjonen, f.eks O i SOA representerer det som skal stå over brøkstreken, og A’en naturlig nok det som skal stå under.
Ved å dele den ene siden på andre får vi et tall som vi kan mate inn i den respektive funksjonen.
Som vi husker fra grafen så kan vi kun bruke et tall mellom 1 og -1, og tallene vi bruker er som regel 0,ettellerannet, fordi sinus til 1 er 90°. Derfor må vi dele det minste tallet på det største, der det største av de to naturligvis alltid er hypotenusen, slik at vi får et tall som er mindre enn 1.
OBS! Denne huskeregelen er i sin normale form kun for å finne vinkler når vi kjenner hypotenusen og en katet. Det vil si, den benytter de inverse funksjonene.
Et eksempel:
Vi skal finne vinkelen X, vi vet hypotenusen og den hosliggende katet.
Basert på dette vet vi at vi må benytte cosinus-funksjonen.
Som vi vet fra huskeregelen, og for å få et forhold under 1, må vi dele kateten på hypotenusen.
Alstå får vi:
Dersom vi behøver å finne en side når vi vet en annen side og vinkelen må vi benytte litt algebra for å gjøre om på formelen.
Vi snur formelen litt, slik at vi kan finne forholdet med funksjonen og gange det med hypotenusen for å få den ukjente.
Slik at det blir:
Ergo får vi:
Hvis du bruker den normale sinusfunksjonen på en vinkel gir den deg et forhold. Bruker du den inverse på et forhold får du en vinkel.
Tangens-funksjonen er i en liten klasse for seg selv.
Som vi ser av huskeregelen er det den eneste av funksjonene som bruker begge katetene i kalkulasjonen.
Hva gjør vi dersom vi kjenner begge katetene og vinkelen, men ikke hypotenusen? Kan vi bruke tangens til å finne den?
Nei, dessverre kan vi ikke det (men sinus og cosinus kan det), ikke direkte hvertfall. Da må vi bruke Pythagoras. Tangens finner ikke lengden av hypotenusen, den finner lengden av streken som går 90° fra hypotenusen på sirkelen og ned til X-aksen. Slik:
Tangens til 60° blir 1,732… og vil da si at lengden av den røde streken er 1,732 ganger hypotenusen.
Som nevnt så er huskeregelen i sin normale form kun for å finne vinkler. Og det kan vi finne ved bruk av tangens.
Ved å dele den motstående på den hosliggende katet får vi et forhold som beskriver vinkelen. Bildet over er et godt eksempel.
Når vinkelen er 45° er sin og cos like, 0,7071… og noe delt på seg selv blir 1. Altså er tangens-streken like lang som hypotenusen.
Når vi nærmer oss 90 vil tangensen bli veldig stor, og for hver desimal du legger på vinkelen vil lengden øke logaritmisk, dvs, tan89,9≈572, tan89,99≈5729, tan 89,999≈57295, et cetera…
tan90 er uendelig og gir en feilmelding hvis du prøver å kalkulere det.
Så for å besvare spørsmålet jeg startet hele kapittelet med; hvorfor skal jeg kunne dette og når kommer jeg til å få bruk for det?
Først å fremst vil det å forstå trigonometri gi deg et nytt syn på verden rundt deg. Ikke det at jeg går rundt å ser sånn Matrix-kode hvor enn jeg går, men jeg legger merke til ymse rariteter som plutselig gir mening fordi jeg ser årsaken til dets design. Som f.eks. at gjengedybde er 0,866 ganger stigningen fordi gjenger er 60 grader og sinus til 60 er 0,866.
Mer praktiske eksempler:
Man kan bruke denne kunnskapen til f.eks å ta et halvt hundredels kutt på dreiebenken ved å stille toppsleiden i 30° i forhold til Z aksen, slik at en hundredels bevegelse på toppsleiden utgjør 0,005mm mating innover, fordi sin30=0,5.
Et annet eksempel er bruk av noe som på engelsk kalles en “sine bar“. Jeg er ikke sikker på hva det kalles på norsk, men en ekvivalent innretning er jo sinusbordet.
“Sinebar”
Sinusbord
Poenget med en “sinebar” - eller sinusbord for den delen - er at du kan oppnå ekstremt eksakte vinkler ved bruk av trigonometri.
Den består av to presist slipte sylindre som er festet til en presisjons-slipt blokk. Avstanden mellom sentere på sylinderne er kjent, alltid et rundt tall som f.eks. 100mm. Streken som går mellom senterne på disse utgjør hypotenusen i trekanten vår og er parallell med overflaten på blokken.
Så ved å bygge oppunder den ene sylinderen kan man øke vinkelen på en presis måte, vanligvis med passbiter.
I eksempelet over, dersom vi vil oppnå en vinkel på 15° må vi finne ut hvor høyt vi skal heve den ene siden.
Basert på lengden mellom aksene til sylinderne, må vi finne forholdet til 15° og gange det med denne lengden.
Sinus til 15 er 0,25881…etc., så dersom vi ganger dette med 100 får vi 25,881 mm. Så hvis vi bygger oppunder den ene sylinderen med 25,881mm vil vinkelen bli nøyaktig 15°.
Bak teppet:
Jeg nevnte at funksjonene er selvstendige funksjoner som gjør jobben sin på en litt skjult måte. Det er én ting å forstå hvordan man bruker dem, men det gir ikke noen dypere forståelse av hvordan selve funksjonene fungerer.
Når det er sagt er funksjonene kompliserte, ikke noe jeg kan gjøre rede for hvordan fungerer i inngående detalj, men det jeg vil poengtere er at de forsøker å gjengi sinuskurven fra en perfekt sirkel, altså approksimere verdiene som oppstår “naturlig“ mellom vinkler og en perfekt sirkel. Vi har ikke egentlig noen perfekt måte å gjengi hvordan en sinuskurve og en sirkel interagerer, men vi har funnet ulike måter å beregne ekstremt nøyaktige tilnærminger. Og det er godt nok. Taylor-serien er en av disse metodene jeg nevnte tidligere:
Under er en graf av Taylor-serien til høyre, og formlene for approksimeringen av sinus og cosinus til venstre. De forskjellige fargene representerer hvor nøye, eller hvor lang vi lager formelen så å si. Jo lenger vi lager formelen jo bedre approksimering av sinuskurven får vi.
Under er en animasjon som viser hvordan vi får en mer korrekt tilnærming jo flere ledd vi legger til i formelen. N = antall ledd.
Jeg går litt vel langt her nå, og snakker om ting som egentlig ikke er relevant for å faktisk bruke funksjonene, men det er fremdeles viktig for å forstå hva de egentlig er. Det er ikke nødvendig å vite dette for å forstå relasjonene og bruken av de trigonometriske funksjonene. Jeg forstår det ikke helt selv, men poenget jeg prøver å få fram er at sinus og cosinus er ikke magiske tall eller forhold, men funksjoner som påvirker tallet du putter inn.
Når du plopper det inn i kalkulatoren bruker den vanligvis noe som kalles for CORDIC-algoritmen. Kalkulatoren jobber som sagt i radianer, men forstår når du skriver ting i grader og viser deg svaret i grader dersom den er satt til det.
Det eneste jeg egentlig har kommet fram til er at jo mer jeg lærer, jo mer forstår jeg at jeg ikke vet.
Men i lys av det jeg nå har skrevet om, og med tanke på mine første paragrafer om skolen og læremetoder, så anbefaler jeg alle å lese Paul Lockhart sitt essay “A Mathematician’s Lament“ .